Unit 1: Scientific Learning – Class 10 Science Guide

unit 1 scientific learning class 10 science guide

DR Gurung

- May 22, 2025 May 25, 2025

Scientific Learning Class 10 Science Guide/Note.

Hello and Welcome to Unit 1 Scientific Learning Class 10 Science Guide/Note. If you are a SEE Class 10 student then you might be searching for SEE Class 10 Science Guide/Note. If so, then you are at right place. The Class 10 Science and Technology Unit 1 is based on the theme "Scientific Learning". SEE Class 10 Science and Technology can be challenging for both students and teachers. To make things easier, we've created a special guide/note that provides solutions to the Unit 1 Scientific Learning Class 10 Science. This unit is based on new curriculum of the year 2077/2078-2082 published by Government of Nepal, Ministry of Education, Science and Technology, Curriculum Development Centre. Credit to "Vidyarthi Pustak Bhandar".

This guide/note of Unit 1 Scientific Learning Class 10 Science and Technology offers detailed answers to every questions - Multiple Choice Questions (MCQs), Differentiate Between, Very Short Question Answers, Short Question Answers, Long Question Answers, Diagrammatic Question Answers, Numerical Problems, etc., helping you understand and master the unit 1. Also, SEE Class 10 Science Notes Unit 1, help you to save your time for searching answers. This note can also be a reference for SEE Preparation. So we're sure that this notes will help you a lot.

Also upon completion of this unit 1 Scientific Learning Class 10 Science Guide/Note, SEE Class 10 students will be able to:

i. Investigate independent variables, dependent variables and control variables in scientific research and mention the importance of the control variable.
ii. Differentiate between fundamental and derived units.
iii. Investigate the fundamental units involved in different derived units.
iv. Mention and use the fundamental units in physical units in physical equation to examine their homogeneity.

Let's explore further key exercises and answers of Unit 1 Scientific Learning Class 10 Science Guide/Note for enhanced learning.

SEE Class 10 Compulsory Science | All Units Notes:

Unit-1 | Scientific Learning | Class 10 | Science | Guide.
Unit-2 | Classifications of Living Beings | Class 10 | Science | Guide.
Unit-3 | Honeybee | Class 10 | Science | Guide.
Unit-4 | Heredity | Class 10 | Science | Guide.
Unit-5 | Psychological structure and Life Process | Class 10 | Science | Guide.
Unit-6 | Nature and Environment | Class 10 | Science | Guide.
Unit-7 | Motion and Force | Class 10 | Science | Guide.
Unit-8 | Pressure | Class 10 | Science | Guide.
Unit-9 | Heat | Class 10 | Science | Guide.
Unit-10 | Wave | Class 10 | Science | Guide.
Unit-11 | Electricity and Magnetism | Class 10 | Science | Guide.
Unit-12 | Universe | Class 10 | Science | Guide.
Unit-13 | Information and Communication Technology (ICT) | Class 10 | Science | Guide.
Unit-14 | Classification of Elements | Class 10 | Science | Guide.
Unit-15 | Chemical Reaction | Class 10 | Science | Guide.
Unit-16 | Gases | Class 10 | Science | Guide.
Unit-17 | Metals and Non-Metals | Class 10 | Science | Guide.
Unit-18 | Hydrocarbon and Its Compounds | Class 10 | Science | Guide.
Unit-19 | Chemicals Used in Daily Life | Class 10 | Science | Guide.

View All SEE Class 10 Compulsory Science Notes:

SEE Class 10 Compulsory Science | All Units Notes and Question Papers Collection.

Scientific Learning

Unit - 1

SEE Class 10 Science Notes.

? Test Your Concepts

1. Multiple Choice Questions (MCQs):

a. Which statement accurately describes the relationship between the rate of photosynthesis and the amount of sunlight in an experiment?

i. Sunlight amount is the dependent variable; photosynthesis rate is the controlled variable.

ii. Sunlight amount is the independent variable; photosynthesis rate is the dependent variable.

iii. Sunlight amount is the controlled variable; photosynthesis rate is the independent variable.

iv. Sunlight amount is the independent variable; photosynthesis rate is the controlled variable.

Answer: ii. Sunlight amount is the independent variable; photosynthesis rate is the dependent variable.

b. Which of the following steps requires five sense organs to detect in scientific learning?

i. making an observation

ii. asking a question

iii. forming a hypothesis

iv. drawing a conclusion

Answer: i. making an observation

c. What is the last, though very significant step in a scientific method that allows other researchers to test the hypothesis.

i. forming a hypothesis

ii. communicating results

iii. drawing a conclusion

iv. making observations

Answer: ii. communicating results

d. What term is used to describe the variable that is dependent on the changes in other variables?

i. responding variable

ii. independent variable

iii. controlled variable

iv. manipulated variable

Answer: i. responding variable

e. In a research project focused on the effects of fertilizers on the growth of garden plants, which factor is expected to be the dependent variable?

i. duration of sunlight exposure

ii. fertilizer brand

iii. height of the plants

iv. soil quality

Answer: iii. height of the plants

f. In an experiment, what term is used to describe the variable that is knowingly altered by the experimenter?

i. dependent variable

ii. constant variable

iii. independent variable

iv. control variable

Answer: iii. independent variable

g. What is the rate of doing work called?

i. power

ii. energy

iii. work

iv. pressure

Answer: i. power

h. Which one of the following is a derived unit?

i. kelvin

ii. mole

iii. hertz

iv. candela

Answer: iii. hertz

2. Differentiate between:

a. independent variables and dependent variables

Answer:

The differences between independent variables and dependent variables are stated below in tabular form:

Independent Variables	Dependent Variables
i. The variables that do not depend on other variables.	i. The variables that depend on other variables.
ii. Independent variables are controllable.	ii. Dependent variables are not controllable.
iii. Explain the cause and effect of changes in the variables.	iii. Explained by the independent variables.
iv. Independent variables are influenced by the researcher.	iv. Changes in response variables are directly caused by the changes in independent variables.
v. Independent variables are exposure variables that are used in the research.	v. Dependent variables are the outcome of the research.

Or,

Aspect	Independent Variable	Dependent Variable
Definition	A variable that is adjusted or modified.	Variable that depends on another for its value.
Role	Alters or influences the dependent variable.	Responds to changes in the relevant variable.
Symbol	Frequently shown in equations as x.	Frequently shown in equations as y.
Example	The amount of fertilizer applied is the independent variable when examining how fertilizer affects plant growth.	Plant growth is the dependent variable in a study on the impact of fertilizer.
Control	It can be manipulated or controlled by the researcher.	Typically, the researcher has less control over it.
Position of Axes in Graphs	Displayed using the x-axis.	Displayed on a y-axis plot.
Purpose in Equations	Examining the effect on the dependent variable is frequently the aim.	Finding its relationship to the independent variable is frequently the aim.

b. fundamental unit and derived unit

Answer:

The differences between fundamental unit and derived unit are shown below in tabular form:

Fundamental Unit	Derived Unit
i. Basic units of measurement that are independent of others.	i. Units that are derived from fundamental units.
ii. Independent; not formed from other units.	ii. Dependent on fundamental unit.
iii. Defined directly by international standards.	iii. Formed by combining two or more fundamental units using mathematical operations.
iv. They are SI Base Units.	iv. They are SI Derived Units.
v. Examples: Meter (m), Kilogram (kg), Second (s), Ampere (A), Kelvin (K), Mole (mol), Candela (cd)	v. Examples: Newton (N), Joule (J), Watt (W), Pascal (Pa), Coulomb (C), etc.

Or,

Fundamental Units	Derived Units
i. Fundamentals units are those units which are independent of any other unit.	i. Derived units are the units that results from a mathematical combination of SI base units.
ii. Fundamental units cannot be further reduced to elementary level; in fact, these are elementary units.	ii. Derived units can be reduced to its elementary level, which are composed of fundamental units.
iii. Fundamental units can not be expressed in terms of derived units.	iii. Derived units can be expressed in terms of derived units.
iv. Only seven fundamental units exist in Metric System or SI system.	iv. There exist a large number of derived units in Metric System.
v. Examples: Length, Mass, Time, Temperature, Electric Current, Luminous Intensity, Amount of Substance.	v. Examples: Velocity, Acceleration, Momentum, Force, Density, Heat, Energy, Power, etc.

c. fundamental quantity and derived quantity

Answer:

The differences between fundamental quantity and derived quantity are shown below in tabular form:

Fundamental Quantity	Derived Quantity
i. Basic physical quantities that are independent of others.	i. Quantities derived from fundamental quantities.
ii. Independent; not derived from other quantities.	ii. Dependent on fundamental quantities.
iii. Examples: Length, Mass, Time, Temperature, Electric Current, etc.	iii. Examples: Speed, Area, Volume, Density, Force, Pressure, etc.
iv. There are only 7 fundamental quantities exist.	iv. There are unlimited (numerous) derived quantities exist.
v. Have their own SI base units (e.g., meter, kilogram, second)	v. Expressed in terms of base units (e.g., m/s, kg/m³, N = kg·m/s²)
vi. Basic form (e.g., [L], [M], [T])	vi. Combination of dimensions (e.g., [M¹L¹T⁻²] for force)

3. Very short answer type questions:

a. What is scientific learning?

Answer:

Scientific learning is the process of gaining knowledge through systematic observation, experimentation, and analysis using the scientific method.

b. What are various steps of scientific learning?

Answer:

The various steps of scientific learning are observation, question, hypothesis, experimentation, analysis, conclusion, and communication of results.

c. What are control variables?

Answer:

Control variables are those variables that are maintained unchanged or constant in an experiment.

d. What are dependent and independent variables in research?

Answer:

In research, the independent variable is the factor that is changed or controlled by the researcher, while the dependent variable is the outcome or effect that is measured.

e. Write clear examples of independent, dependent, and controlled variables.

Answer:

The clear example of independent, dependent, and controlled variables is -

Example: In an experiment testing how sunlight affects plant growth:
Independent variable: Amount of sunlight.
Dependent variable: Plant height.
Controlled variables: Water, soil type, and plant species kept the same.

f. What are the independent, dependent, and controlled variables in an experiment investigating the reaction rate between calcium carbonate and dilute hydrochloric acid?

Answer:

In the experiment investigating the reaction rate between calcium carbonate and dilute hydrochloric acid:
Independent variable: Concentration of hydrochloric acid.
Dependent variable: Rate of reaction (e.g., amount of gas produced over time).

Controlled variables: Amount and surface area of calcium carbonate, volume of acid, temperature, and pressure.

g. State the principle of homogeneity of equations.

Answer:

The principle of homogeneity of equations is "an equation is correct if the dimensions of all terms on both sides of the equation are the same".

h. Which physical quantity is represented by kg/m³?

Answer:

The physical quantity represented by kg/m³ is density, which is the mass per unit volume of a substance.

i. If a zoologist is turning a bulb on and off to observe the movement of a cockroach, what would be considered the independent variable in this experiment?

Answer:

In this experiment, the independent variable would be the state of the bulb (on or off), as it is being manipulated to observe its effect on the cockroach's movement.

j. Define fundamental and derived units.

Answer:

Fundamental units are basic units of measurement defined by the SI system (e.g., meter, kilogram, second), while derived units are formed by combining fundamental units (e.g., m/s for speed, kg/m³ for density).

k. Define a unit. Write its types.

Answer:

A unit is a standard quantity used to measure physical properties like length, mass, or time. The types of units are - (i) Fundamental Units and (ii) Derived Units.

l. Name the fundamental units used in physics.

Answer:

The fundamental units used in physics are metre (m), kilogram (kg), second (s), ampere (A), kelvin (K), mole (mol) and candela (cd).

Or,

The seven fundamental units used in physics (SI units) are:
Meter (m) – for length
Kilogram (kg) – for mass
Second (s) – for time
Ampere (A) – for electric current
Kelvin (K) – for temperature
Mole (mol) – for amount of substance
Candela (cd) – for luminous intensity

4. Short answer type questions.

a. What are variables in research? Explain with examples.

Answer:

Many factors that can affect the outcomes or results of experiments are called variables.

Example: 1 -

Research Question: Does listening to music while studying affect memory recall?
i) Independent Variable: Listening to music (yes/no).
ii) Dependent Variable: Memory recall score.
iii) Controlled Variables: Study time, difficulty of material.

Or,

Example: 2 -
Research Question: In a study examining the effect of study time.
i) Independent Variable: the amount of the study time.
ii) Dependent Variable: the test scores.

iii) Controlled Variables: the study environment.

b. Clarify different types of variables giving an example of experiment.

Answer:

The different types of variables are - Independent variable, Dependent variable and Controlled variable.

Example - Experiment: Does drinking caffeine affect reaction time in adults?

i) Independent Variable: Amount of caffeine consumed (e.g., no caffeine, 100mg, 200mg).
ii) Dependent Variable: Reaction time (measured in milliseconds using a computer test).

iii) Controlled Variables: Time of day, test used, sleep before testing.

c. What is the dimension of a physical quantity? Give an example.

Answer:

The dimension of a physical quantity refers to the powers (or exponents) of the fundamental physical quantities (like mass, length, and time) that are used to express that quantity.
Example: Force

Force is defined by Newton's second law:

Force = Mass \times Acceleration

Mass → [M]
Acceleration → $\frac{Length}{Time²} = [L] [T⁻²]$

So,

Dimension of Force = [M] [L] [T⁻²]

✅ Final Answer:

The dimension of force is $M L T⁻²$ .

d. Why is the independent variable referred to as the predictor variable, and the dependent variable as the responding variable?

Answer:

The independent variable is referred to as the predictor variable because it is used to forecast or predict the outcome of the dependent variable. The dependent variable is referred to as the responding variable because it is what changes or responds in reaction to changes in the independent variable.

e. Why is the joule the SI unit of work and energy?

Answer:

The joule (J) is the SI unit of work and energy because it is defined based on fundamental units in the International System of Units (SI), and it reflects how work and energy are quantified in physics.

Tips🔺:

🔅 Define/What is a Joule?

Answer: 1 joule (J) is the work done when a force of 1 newton moves an object 1 meter in the direction of the force.

1 J = 1 N \cdot 1 m = 1

kg.m²/s²

🔅 Why is the Joule used for both Work and Energy?

Answer: The Joule (J) is used for both Work and Energy because work and energy are closely related as below:
- Work is the process of transferring energy.
- When work is done, energy is transferred or transformed.

- Both involve the same physical quantity and unit (energy transfer or change), so they share the unit joule.

f. Why is the unit of power referred to as a derived unit?

Answer:

The unit of power is referred to as a derived unit because it is not a fundamental unit by itself. Instead, it is derived from basic (fundamental) SI units - specifically, from the definitions of work (or energy) and time.

Tips🔺:

Power = Work/Time

We know,

Work is measured in joules (J) and Time in seconds (s).

So, Power = J/s = kg.m²/s³ [J = kg.m²/s²]

→ The SI unit of power is the watt (W):

Therefore, 1W = 1 joule/second = 1 kg.m²/s³

Summary
Quantity	Formula	Unit	Derived From
Power	Work ÷ Time	Watt (W)	kg·m²/s³ (derived from J/s)
Work	Force × Distance	Joule (J)	kg·m²/s²

g. The unit of pressure is a derived unit, why?

Answer:

The unit of pressure is called a derived unit because it is not a fundamental unit on its own - it is derived from fundamental SI units through a physical relationship involving force and area.

Tips🔺:

Pressure = Force/Area

We know,

Force is measured in Newton (N) and Area is measured in square metres (m²).

So, Pressure = N/m² = 1kg⋅m/s²/m² = kg/m.s² [1N = 1kg⋅m/s²]

Therefore, this derived unit is called Pascal (Pa).

1 pascal (Pa) = 1 newton per square meter (N/m²)

1Pa = 1kg⋅m⁻¹⋅s⁻²

h. Why is it important to consider controlled variables in scientific research?

Answer:

It's very important to consider controlled variables in scientific research to ensure that your results are valid, reliable, and accurate. Here's why:

i) to ensure a fair test.

ii) to reduce error and bias.

iii) to improve reliability and reproducibility.

iv) to accurately identify cause and effect.

i. Why is it not permissible to add or subtract physical quantities with different basic units?

Answer:

It is not permissible to add or subtract physical quantities with different basic units because they represent different types of measurements - they are not comparable in a meaningful or physically valid way.

Let say - In case of s + at, the first term represents displacement, whose unit is metre (m), and the second term represents acceleration multiplied by time, whose unit is (ms⁻².s or ms⁻¹). It is not valid to add or subtract different fundamental quantities with different unit, i.e. m and ms⁻¹.

j. What is the unit of work? Explain whether the unit of work is a fundamental or derived unit?

Answer:

The SI unit of work is Joule (J). The unit of work is derived unit. The unit of work is a derived unit because it is made from the multiplication of other fundamental units.

Let's see -

We know,

Work is defined as: Work = Force x Distance

where Force is measured in newtons (N), which is itself a derived unit. (1N = 1 kg.m/s²) and Distance is measured in Metres (m).

So, the unit of Work becomes:

1 Joule (J) = 1 N.m = 1kg.m²/s²

Tips🔺:

🔅 Why is the unit of work is a derived unit?

Answer: The unit of work (joule) is a derived unit because it is made from the multiplication of other fundamental units: kg.m²/s².

k. Why the unit of force is called a derived unit?

Answer:

The unit of force is called a derived unit because it is not fundamental and it is derived from other fundamental quantities.

Or,

The unit of force is a derived unit because it is constructed from fundamental units - mass, length, and time - rather than being a basic, standalone quantity.

Let's see -

We know,

Force (F) = Mass (m) x Acceleration (a)

Here, Mass (m) is fundamental quantity, measured in kilogram (kg) whereas Acceleration (a) is the rate of change of velocity and measured in metre per second square (m/s²).

So,

Force = kg x m/s²

Hence, the unit is named newton (N):

1N = 1kg.m/s²

l. What is a derived unit? Give its two examples.

Answer:

A derived unit is a unit of measurement that is formed by combining two or more fundamental units. The two examples of derived unit are -

a. Newton (N) - the unit of Force: 1N = 1kg.m/s²

b. Joule (J) - the unit of Work or Energy: 1J = 1N.m = 1kg.m2/s2

m. Define measurement and unit.

Answer:

Measurement is the process of comparing an unknown physical quantity with a standard known quantity. For examples:- measuring length: 5 meters, measuring mass: 2 kilograms, etc.

A unit is a standard quantity used to express a measurement. For examples:- meter (m) is the unit of length, kilogram (kg) is the unit of mass, second (s) is the unit of time, etc.

n. Write the SI units of the following physical quantities:

i. potential difference

ii. electrical resistance

iii. temperature

iv. amount of substance

Answer:

The SI units of the following physical quantities are -

Physical Quantity	SI Unit	Symbol
i. Potential Difference	Volt	V
ii. Electrical Resistance	Ohm	Ω
iii. Temperature	Kelvin	K
iv. Amount of Substance	Mole	mol

o. Point out the fundamental and derived units from the units given below:

joule, watt, hertz, second, Pascal, Kelvin, mole, Newton

Answer:

The fundamental and derived units from the above listed units are answered below -

i. joule (J) - derived unit

ii. watt (W) - derived unit

iii. hertz (Hz) - derived unit

iv. second (s) - fundamental unit

v. Pascal (Pa) - derived unit

vi. Kelvin (K) - fundamental unit

vii. mole (mol) - fundamental unit

viii. Newton (N) - derived unit.

Or,

Tabular form:

Fundamental Units	Derived Units
second (s)	joule (J)
Kelvin (K)	watt (W)
mole (mol)	hertz (Hz)
	Pascal (Pa)
	Newton (N)

5. Long answer type questions.

a. Explain the functions of variables in a scientific experiment.

Answer:

In a scientific experiment, variables play important roles in helping us understand how changes in one factor affect another. Each type of variable has a specific function that contributes to the reliability, clarity, and validity of the experiment.

Types and Functions of Variables:
i. Independent Variable
Function: It is the variable that the experimenter changes or manipulates to observe its effect.
Purpose: To test its impact on the dependent variable.
Example: Changing the length of a ramp (effort distance) in an experiment.
ii. Dependent Variable
Function: It is the variable that is measured or observed during the experiment.
Purpose: To see how it responds to changes in the independent variable.
Example: Measuring the amount of force (effort) needed to move a load.
iii. Controlled Variables (Constants)
Function: These are variables that are kept the same throughout the experiment.
Purpose: To ensure a fair test and isolate the effect of the independent variable.
Example: Keeping the weight of the load and the surface material constant.
iv. Extraneous Variables (optional mention)
Function: These are unwanted variables that might affect the results if not controlled.
Purpose: To minimize error and improve experimental accuracy.
Example: Friction, air resistance, or temperature changes.

b. Enlist the characteristics of standard units.

Answer:

The important characteristics of standard units in list form are -
i. They are Universally Accepted - A standard unit must be accepted and used globally to ensure consistency in measurements.
ii. They are Well-Defined - It should have a clear and unambiguous definition, ensuring that the unit can be precisely and accurately reproduced.

iii. They are Invariable - A standard unit must not change with time, location, or environmental conditions (like temperature or pressure).
iv. They are easily Reproducible - It should be possible to reproduce the standard unit easily and accurately anywhere in the world.
v. They are convenient in Size - The unit should be of a magnitude that is practical for everyday use and scientific work (not too large or too small).
vi. They are Independent of Physical Objects (Ideally) - Modern standard units should be based on fundamental constants of nature rather than physical artifacts, to avoid variability.
vii. They are compatible with Derived Units - The standard units should support the derivation of other units (e.g., Newton for force, derived from kilogram, meter, and second).

c. What are the fundamental units involved in the following derived units?

i. Pascal

ii. Hertz

iii. Newton
iv. Watt

Answer:

The fundamental units involved in the derived units pascal, hertz, newton and watt are -

🔀 i. Pascal

✅ Here:

Pascal (Pa) = Unit of Pressure.

We know,

1 Pa = 1 N/m²

Fundamental units:

Pa = kg.m/s²╱m² [∵N = kg.m/s²]

Pa = kg╱ms²

Pa = kg.m⁻¹.s⁻²

∴ Pascal (Pa) = kg.m⁻¹.s⁻²

🔀 ii. Hertz

✅ Here:

Hertz (Hz) = Unit of Frequency.

We know,

1 Hz = 1 cycle/second

Fundamental units:

Hz = 1/s

Hz = s⁻¹

∴ Hertz (Hz) = s⁻¹

🔀 iii. Newton

✅ Here:

Newton (N) = Unit of Force.

We know,

1 N = 1 kg·m/s²

Fundamental units:

N = kg.m.s⁻²

∴ Newton (N) = kg.m.s⁻²

🔀 iv. Watt

✅ Here:

Watt (W) = Unit of Power.

1 W = 1 J/s = 1 N.m/s

Fundamental units:

W = kg.m/s² × m/s [∵ N = kg.m/s²]

W = kg.m².s⁻³

∴ Watt (W) = kg.m².s⁻³

d. Why are dimensional equations important in the field of science?

Answer:

Dimensional equations are important in the field of science because they help us as a powerful tool for consistency checks, unit conversions, and problem-solving across various scientific and engineering disciplines. Below are the few key reasons -

i. Converting units - They assist in unit conversion, especially between different systems of measurement (e.g., CGS to SI), ensuring consistent and accurate results.

ii. Deriving relationships between physical quantities - Using dimensional analysis, scientists can derive relationships between physical quantities even when the exact formula is not known, by analyzing how units relate to one another.

iii. Predicting new physical quantities - By analyzing the dimensional form, scientists can predict the form of new physical quantities and propose possible equations that describe physical phenomena.

iv. Checking the correctness of equations - They help to verify whether a physical equation is dimensionally consistent. If both sides of the equation do not have the same dimensions, the equation is definitely incorrect.

v. Ensuring dimensional homogeneity - They ensure dimensional homogeneity in physical laws and equations - an essential condition for the validity of any physical expression.

vi. Scaling and modeling - They help in scaling models to real-world systems, especially in fluid dynamics, astrophysics, and aerodynamics in engineering and physics.

Or,

Answer:
Dimensional equations are important in the field of science because they help us to understand the relationships between different physical quantities. By analyzing the dimensions (such as length, time, mass, etc.) of various physical quantities involved in an equation, we can check the consistency of the equation and verify if the derived formula is correct. This helps in avoiding errors and ensures accuracy in scientific calculations and theories.

e. What are the limitation of unit-wise analysis of physical equation in science?

Answer:

Unit-wise (or dimensional) analysis is a powerful tool in science, but it has several limitations. Here are the main limitation of unit-wise analysis of physical equation in science:-

i. Cannot determine dimensionless constants - Dimensional analysis cannot determine numerical constants like 2, π, or 1/2 in equations. For example, it can't show that the area of a circle is exactly πr².
ii. Only applicable to dimensionally homogeneous equations - It can only be applied to equations that are dimensionally homogeneous, meaning all terms must have the same dimensions. It can't be used to analyze equations that mix dimensionless and dimensional quantities improperly.
iii. Fails for trigonometric, exponential, or logarithmic functions - Dimensional analysis does not work when dealing with functions like sin(θ), e^x, or log(x), because their arguments must be dimensionless, and the method can’t handle these forms properly.
iv. Cannot distinguish between vector and scalar quantities - Unit-wise analysis does not differentiate between vector and scalar quantities, even though their physical meanings and behaviors are different.
v. Cannot predict functional form accurately - Although it can suggest a possible relationship between variables, it cannot provide the exact form of the equation - such as whether it's linear, quadratic, or involves higher powers.
vi. Inapplicable to empirical or experimentally derived laws - Some physical laws are purely empirical (e.g., Ohm’s Law or Boyle’s Law), and dimensional analysis cannot derive or verify them from first principles.

Or,

Answer:
Unit-wise (or dimensional) analysis of physical equations involves checking if the units on both sides of an equation are consistent. While this method is useful for catching simple errors, it has limitations. One limitation is that it does not account for the numerical values or coefficients in the equation. Secondly, it may overlook more complex dimensional inconsistencies that could lead to incorrect conclusions. Thirdly, it cannot distinguish between scalar and vector quantity. Fourthly, it does not provide extra details about the constant in the equation. And also it fails for trigonometric, exponential or logarithmic functions. Therefore, relying solely on unit-wise analysis without considering the actual dimensions of the quantities involved can be misleading.

f. Using the principle of homogeneity, evaluate the accuracy of the physical equation s = ut +1/2 at². In the equation, s stands for displacement, u for initial velocity, t for time, and a for acceleration.

Answer:

To evaluate the accuracy of the physical equation s = ut +1/2 at² using the principle of homogeneity, we need to check whether all terms have the same dimensions (i.e., whether the equation is dimensionally homogeneous). And, here is the detailed steps -

Step 1: Identify the dimension of each quantity.

s (Displacement) = [L]

u (Initial Velocity) = [LT⁻¹]

t (Time) = [T]

a (Acceleration) = [LT⁻²]

Step 2: Analyze the dimensions of each term in the equation.

Left-hand side (LHS):

s = [L]

Right-hand side (RHS):

ut +1/2 at²

First Term = ut = [LT⁻¹].[T] = [L]

Second Term = 1/2 [LT⁻²].[T]² [∵ The constant 1/2 is dimensionless, we ignore it in dimensional analysis.]

So, Second Term = [LT⁻²].[T]² = [L]

Step 3: Comparing the dimensions.

LHS = [L]

RHS = [L] + [L] = [L]

Hence, all terms have the same dimension, so the equation is dimensionally homogeneous.

Conclusion:

The equation s = ut +1/2 at² is dimensionally accurate according to the principle of homogeneity. This means the form of the equation is likely correct, though this method does not confirm numerical constants like 1/2.

g. Hari conducted an experiment to see how catalysts A, B and C affect chemical reaction rates. He used the same reactants but tested at different temperatures for a fixed time. Answer the following questions based on the experiment.

i. What are the variables in Hari's catalyst experiment?

ii. Why did Hari use the same reactants and only changed the type of catalysts?

iii. Why were different temperatures used in the reactions conducted by Hari?

Answers:

i. What are the variables in Hari's catalyst experiment?

Answer: The variables in Hari's catalyst experiment are :-

Independent variables - The type of catalyst used (Catalyst A, B, or C).

Dependent variables - The rate of the chemical reaction.
Controlled (constant) variables - The reactants used, the reaction time, Other conditions (e.g., pressure, volume, concentration - if not intentionally varied).
Experimental condition that varied additionally - Temperature, which appears to be intentionally changed for further analysis.

ii. Why did Hari use the same reactants and only changed the type of catalysts?

Answer: Hari used the same reactants to ensure that any change in the reaction rate was due only to the effect of different catalysts. This approach isolates the catalyst as the only changing factor, which allows for a fair comparison of how each catalyst influences the reaction.

iii. Why were different temperatures used in the reactions conducted by Hari?
Answer: Different temperatures were likely used to study how temperature affects the activity of each catalyst. Since catalysts often have temperature-dependent performance, Hari might have wanted to find:
- The optimal temperature for each catalyst.
- How each catalyst behaves under different thermal conditions.
This helps to provide a more complete understanding of each catalyst's effectiveness.

h. Raman wants to investigate which colour of an object has the highest capacity to absorb heat. He took four tin cans and painted them with black, white, green and red colours respectively. He poured an equal amount of water into each can, closed the openings, and placed them in sunlight for an hour. After that, he measured the temperature of the water in each can using a thermometer. Answer the following questions based on the experiment.

i. Write the independent and dependent variables.

ii. Which variables should be controlled by Raman? Explain.

iii. What is the hypothesis of this experiment?

iv. How will Raman ensure that the temperature measurements are accurate?

v. How might Raman extend this experiment to test other factors that affect the absorption of heat by an object?

Answer: Below are the answers to the questions based on Raman's heat absorption experiment:-

i. Write the independent and dependent variables.

Answer: The independent and dependent variables are -
☄ The colour of the tin cans (black, white, green, red) - Independent Variable.
☄ The temperature of the water in each can after exposure to sunlight - Dependent Variable.

ii. Which variables should be controlled by Raman? Explain.

Answer: Raman should control the following variables to ensure a fair test:

☄ Amount of water in each can – should be equal to ensure consistent heat capacity.
☄ Type and size of the cans – identical material and dimensions so the only difference is the colour.
☄ Exposure to sunlight – place all cans in the same location to receive equal sunlight.
☄ Duration of exposure – all cans must remain in the sun for exactly the same time (1 hour).
☄ Initial temperature of water – should be the same in each can before starting the experiment.
☄ Lid or cover – use similar lids to prevent heat loss and ensure uniform conditions.
These controls help ensure that only the colour is influencing the temperature change.

iii. What is the hypothesis of this experiment?

Answer: The hypothesis of this experiment is "The black-coloured can will absorb the most heat and therefore have the highest water temperature after one hour in the sun."

(This is based on the scientific principle that darker colours absorb more heat than lighter colours.)

iv. How will Raman ensure that the temperature measurements are accurate?

Answer: Raman will ensure that the temperature measurements are accurate by following ways:

☄ Using a reliable and calibrated thermometer for each reading.
☄ Measuring immediately after removing the cans from sunlight to avoid heat loss.
☄ Inserting the thermometer to the same depth in each can.
☄ Taking multiple readings for each can and calculating the average.
☄ Ensuring the thermometer is not touching the sides or bottom of the can, which may affect the reading.

v. How might Raman extend this experiment to test other factors that affect the absorption of heat by an object?

Answer: Raman might extend this experiment to test other factors that affect the absorption of hear by an object by following ways:

☄ Test different materials of cans (e.g., aluminum, plastic, glass) while keeping the colour constant.
☄ Vary the surface texture (e.g., matte vs. glossy) to see if that influences absorption.
☄ Change the time of exposure (e.g., 30 mins, 2 hours) to analyze rate of temperature increase.
☄ Use different light sources (e.g., artificial lamps vs. natural sunlight).
☄ Compare open vs. closed cans to study heat loss.
☄ Add insulating materials to test their effectiveness in preventing heat gain.

i. Why are independent and dependent variables important in scientific study?

Answer:

Independent and dependent variables are important in scientific studies because they allow researchers to design clear experiments, test hypotheses, and draw meaningful conclusions. Here is why they are important:
1. Clarify Cause-and-Effect Relationships:
☄ The independent variable is what the scientist changes or controls.
☄ The dependent variable is what is measured or observed.
☄ This setup helps scientists determine whether changes in the independent variable cause changes in the dependent variable.
2. Guide Experimental Design:
☄ Identifying variables helps researchers:
☄ Set up a controlled and focused experiment
☄ Decide what to measure and how to measure it
☄ Keep other factors constant to ensure valid results
3. Enable Data Collection and Analysis:
☄ Knowing which variable is dependent allows for proper data tracking and comparison.
☄ Data can be visualized in graphs (e.g., dependent variable on the y-axis vs. independent variable on the x-axis) to observe trends.
4. Support Reproducibility:
☄ Clear identification of variables helps other scientists replicate the experiment and verify the findings.
☄ This is critical for building reliable scientific knowledge.
5. Test Hypotheses:
☄ Hypotheses are usually framed as predictions about how changing one variable (independent) will affect another (dependent).
☄ Accurate identification of these variables is essential to scientific reasoning and hypothesis testing.

In summary, Independent and dependent variables are key tools for Understanding relationships, Designing sound experiments, Collecting accurate data, Reaching valid conclusions, etc. They form the backbone of scientific inquiry.

j. Can you include more than one independent and dependent variable in scientific study?

Answer: Yes, we can include more than one independent and dependent variable in scientific study but it requires careful planning to ensure the results are valid and interpretable. Multiple independent variables allow researchers to explore the combined or interacting effects of different factors on an outcome, while multiple dependent variables allow for a more comprehensive understanding of the outcome by measuring various facets of it.

Elaboration:

1. Multiple Independent Variables:
Researchers may include more than one independent variable to study:
☄ How each factor individually affects the outcome?
☄ How the variables interact with each other?
Example:
Studying plant growth with:
☄ Amount of sunlight (first independent variable)
☄ Type of fertilizer (second independent variable)
This setup allows you to explore:
☄ The effect of each variable on growth
☄ Whether the combination of sunlight and fertilizer has a unique effect
This type of design is called a multifactorial or factorial experiment.
2. Multiple Dependent Variables:
A study can also have more than one dependent variable, especially if you're interested in observing several outcomes.
Example:
In a health study testing a new drug, dependent variables could include:
☄ Blood pressure
☄ Heart rate
☄ Cholesterol level
Each of these outcomes provides a different way to evaluate the drug’s effectiveness.

⚠️ Things to Consider
☄ Complexity increases: Managing multiple variables can make the experiment and data analysis more complex.
☄ Control is essential: You must carefully control other variables to isolate the effects of your independent variables.
☄ Statistical analysis: Advanced statistical tools (e.g., ANOVA, regression) are often needed to analyze the effects accurately.

k. Proof that:

i. The unit of power (W) = kg.m².s⁻³.

ii. The unit of electric resistance Ohm (Ω) = kg.m².s⁻³.A⁻².

iii. The unit of force (N) = kg.m.s⁻².

Answer:

i. The unit of power (W) = kg.m².s⁻³.

✅ Answer:

By definition: Power = Work (J)/Time (s) =Energy (J) /Time (s)

Work or energy is measured in joules (J), and:

1J = 1 N.m

1J = 1 kg⋅m/s².m [∵ From the force definition 1 N=1 kg⋅m/s²]

So,

1J = 1 kg⋅m²/s²

Now for power:

1W = 1J/1s = 1 kg⋅m²/s²╱s = 1 kg⋅m²/s³

Therefore, the unit of power (W) = kg.m².s⁻³

ii. The unit of electric resistance Ohm (Ω) = kg.m².s⁻³.A⁻².

✅ Answer:

By Ohm's Law: Electric Resistance (R) = V/I

Voltage V is measured in volts (V)
Current I is in amperes (A)
1 volt (V) is defined as:

1 V = 1W/1A [W = Unit of Power]

1V = 1kg.m².s⁻³/A [1W = 1kg.m².s⁻³]

So, 1V = 1kg.m².s⁻³.A⁻¹

Now, Resistance (R) = V/A = 1kg.m².s⁻³.A⁻¹/A = kg.m².s⁻³.A⁻²

Therefore, the unit of electric resistance Ohm (Ω) = kg.m².s⁻³.A⁻²

iii. The unit of force (N) = kg.m.s⁻².

✅ Answer:

Definition from Newton’s Second Law:

Force (F) = Mass (m) x Acceleration (a)

Where Mass (m) is in kg and Acceleration (a) is in m/s².

So,

1 N = 1 kg . m/s² = kg.m.s⁻²

Therefore, the Unit of force (N) = kg·m·s⁻²

l. Analyse the following equations unit-wise to prove whether it is valid or not.

i. s = ut + 1/2 at²

ii. v²-u² = 2a².s

Answers:

i. s = ut + 1/2 at²

Answer:

This is a standard equation of motion. Let's analyze its units:

s: displacement → unit = m
u: initial velocity → unit = m/s
t: time → unit = s
a: acceleration → unit = m/s²

Now,

Left-hand side (LHS):

s = [m]

Right-hand side (RHS):

First term - ut = [m/s] x [s] = [m]

Second term - 1/2 at² = [m/s²] x [s²] = [m] [∵ The constant 1/2 is dimensionless, we ignore it in dimensional analysis.]

Adding both terms,

[m] + [m] = [m]

Hence, LHS = RHS

Therefore, Equation is valid dimensionally.

ii. v²-u² = 2a².s

Answer:

Here,

v,u: velocity → unit = m/s

a: acceleration → unit = m/s²

s: displacement → unit = m

Now,

Left-hand side (LHS):

v²-u² = [m/s]² - [m/s]² = [m/s]² = m²s²

Right-hand side (RHS):

2a².s = a².s = [m/s²]².m = m²s⁴.m = m³s⁴

So, LHS = m²s² and RHS = m³s⁴ do not match.

Units do not match. Therefore, equation is not valid dimensionally.

m. Controlled variables are important in scientific learning. Why?

Answer: Controlled variables are important in scientific learning because they ensure that an experiment is fair, reliable, and focused. Here is why they are important:

1. Ensure a Fair Test:
☄ Controlled variables are the factors that are kept constant throughout an experiment.
☄ By controlling these, you make sure that the only thing affecting the outcome is the independent variable.
☄ This allows you to accurately test cause and effect.
2. Increase Accuracy and Reliability:
☄ Controlling variables reduces errors and variability in results.
☄ This makes your experiment more precise and repeatable by others.
3. Avoid Confounding Factors:
☄ If multiple variables change at once, it’s unclear which one caused the observed result.
☄ Controlled variables eliminate these confounding factors, keeping the experiment focused and meaningful.
4. Support Valid Conclusions:
☄ Only by keeping other variables constant you can confidently say that the independent variable caused the change in the dependent variable.
☄ This leads to more credible scientific conclusions.

n. Why can independent variables be manipulated but not dependent variables?

Answer: Independent variables can be manipulated because they are the "cause" in an experiment, while dependent variables cannot be manipulated because they are the "effect."

1. Independent Variable = What You Change:
☄ The independent variable is under the control of the experimenter.
☄ You manipulate it on purpose to see how it affects something else.
Example: In an experiment to see how light affects plant growth, the amount of light is the independent variable.
You choose to expose one plant to 2 hours of light, another to 4, and another to 6.
2. Dependent Variable = What You Measure:
☄ The dependent variable is what you observe or measure in response to the changes you made to the independent variable.
☄ You do not manipulate it — it changes on its own based on what you did to the independent variable.
Continuing the example: You measure the height of each plant. That’s your dependent variable.
You don’t control how tall they grow — you just record the result.
⚠️ Why not manipulate the dependent variable?
🔖Because the experiment wouldn’t test anything!
☄ If you manually adjust or influence the dependent variable, it no longer reflects the effect of the independent variable.
☄ You can’t learn about cause and effect if you interfere with the outcome you're trying to observe.

o. Why is it important for a scientist to communicate the results and conclusions of a study?

Answer: It is very important for a scientist to communicate the results and conclusions of a study because this is how science advances, becomes useful, and stays credible. Here are the main reasons:

1. Allows Others to Verify the Findings:
☄ When scientists share their methods and results, others can repeat the experiment to confirm its accuracy.
☄ This process is called replication, and it helps build trust and reliability in scientific knowledge.
2. Contributes to the Body of Knowledge:
☄ Science is a collaborative effort.
☄ By sharing findings, a scientist adds to what is already known, helping others build on their work or avoid repeating the same experiment.
3. Encourages Peer Review and Feedback:
☄ Communicating results through papers, presentations, or reports allows other experts to evaluate the work.
☄ Peer review helps catch mistakes, improve quality, and ensure the conclusions are supported by evidence.
4. Solves Real-World Problems:
☄ Scientific research often leads to solutions in medicine, engineering, agriculture, technology, and more.
☄ If results aren't communicated, society misses out on important discoveries and innovations.
5. Informs Policy and Public Decisions:
☄ Scientific findings guide decisions about health, environment, safety, education, and many other areas.
☄ Sharing results ensures that governments, organizations, and the public make choices based on solid evidence.
6. Inspires Further Questions and Research
☄ Every experiment opens the door to new questions.
☄ Sharing results helps other scientists identify new areas to explore, leading to continuous progress.

6. Diagrammatic questions:

In the experiment below, a researcher is testing the effect of effort distance of the slanted surface on the effort applied to lift up the load.

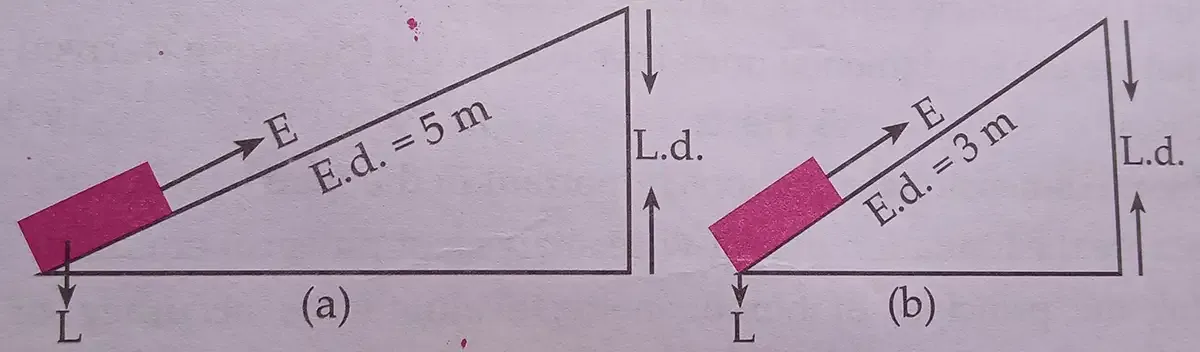Experiment - Effect of effort distance of the slanted surface on the effort applied to lift up the load.

i. What variables are involved in it?

Answer: The variables involved in it are -

(a) Effort Distance (E.d.) – the length of the inclined plane (5 m in (a), 3 m in (b)).

(b) Effort (E) – the force applied to move the load up the plane.

(d) Load Distance (L.d.) – the vertical height to which the load is raised.

(e) Incline Angle – changes as E.d. changes, affecting the amount of effort.

(f) Friction – can influence the effort required (may be assumed negligible or constant).

ii. Which variables have to be controlled in the experiment?

Answer: The following variables have to be controlled in the experiment -

(a) Load (L) – same weight in both setups.
(b) Load Distance (L.d.) – same vertical height in both cases.
(c) Surface type and friction – use the same material and maintain conditions.
(d) Inclined plane width – same size platform.
(e) Measurement tools – same force meter, etc.

iii. Sort out independent, dependent and combined variables in it.

Answer:

Independent Variable: Effort Distance (E.d.) – varied (5 m vs 3 m).

Dependent Variable: Effort (E) – measured to see how it changes with E.d.

Controlled Variables: Load (L), Load Distance (L.d.), surface material, friction.

Combined/Derived Variable: Mechanical Advantage (MA) = L.d. / E.d.; Work Done = E × E.d. (constant if friction is negligible).

Extra Tips: ⛄

Fundamental Units (Basic Units) and Dimensions of Fundamental Units.

What are Fundamental Units? Write unit (SI) and Dimension Symbol of Fundamental Units.

Write the Dimensions of Fundamental Units.

Physical Quantity	Unit (SI)	Dimension Symbol
Length	meter (m)	L
Mass	kilogram (kg)	M
Time	second (s)	T
Temperature	kelvin (K)	Θ (Theta)
Electric Current	ampere (A)	I
Luminous Intensity	candela (cd)	J
Amount of Substance	mole (mol)	N

Derived Units and their relation with Fundamental Units.

S.N.	Derived Quantity	Related Formulae	Symbol of Unit Name	Derived Units	Fundamental Units Involved
1.	Area (A)	length×breadth (l×b)	square metre	m²	m×m
2.	Volume (V)	length×breadth×height (l×b×h)	cubic metre	m³	m×m×m
3.	Velocity (v)	displacement/time (s/t)	metre per second	ms⁻¹	m/s
4.	Acceleration (a)	change in velocity/time (v-u/t)	metre per square second	ms⁻²	m/(s×s)
5.	Force (F)	mass×acceleration (m×a)	kilogram×metre per square second or Newton	N	kg×m/(s×s)
6.	Density ( $ρ$ or d)	mass/volume (m/v)	kilogram per cubic metre	kg/m³ or kgm⁻³	kg/(m×m×m)
7.	Pressure (P)	force/area (F/A)	Newton per square metre or Pascal	Pa or Nm⁻²	kg/(m×s×s)
8.	Momentum (p)	mass×velocity (m×v)	kilogram×metre per second	kgms⁻¹	kg×m/s
9.	Work and Energy (W/E)	force×displacement (F×s)	Newton×metre or joule	Nm or J	(kg×m×m)/(s×s)
10.	Power (P)	workdone/time (w/t)	Joule per second or watt	Js⁻¹ or W	(kg×m×m)/(s×s×s)
11.	Frequency (f)	velocity/wavelength (v/λ)	1/second or Hertz	Hz	cycle/s or s⁻¹
12.	Potential Difference (V)	work done/charge (w/q)	newton×metre/Columb (second×Ampere) or volt (J/C)	V	(kg×m×m)/(s×s×s×A)
13.	Resistance (R)	potential difference/current (V/I)	Newton×metre/columb×second×Ampere Or ohm	Ω	(kg×m×m)/(s×s×s×A×A)

6. The unit of Area is a derived unit. Justify.

Answer:

Here,

Area is defined as the amount of space within a two-dimensional boundary.
Mathematically, for a rectangle, Area = length × width.
Both length and width are measured in the base unit of metres (m) in the SI system.
Therefore,

The unit of area is: metre×metre = metre² = m²
Since m² is formed by combining the base unit metre (m), the unit of Area is derived unit.

7. The unit of Volume is a derived unit. Justify.

Answer:

Here,

Volume is defined as the amount of space occupied by a three-dimensional object.
For a cube or rectangular prism,

Volume = length × width × height.
Each of these dimensions is measured in the base unit of length, which is the metre (m) in the SI system.
So, the unit of volume becomes:

metre × metre × metre = m³

Since, m³ is obtained by combining the base unit metre three times (raised to the power of 3), Volume is a derived unit.

8. The unit of Velocity is a derived unit. Justify.

Answer:

Here,

Velocity is defined as the rate of change of displacement with respect to time.

Mathematically,

Velocity = Displacement/Time
In the SI system:
Displacement is measured in metres (m) → a base unit of length.
Time is measured in seconds (s) → a base unit of time.
So,

The unit of velocity becomes: metre/second = m/s = ms⁻¹

The unit of velocity combines two base units, so it is not a base unit itself, but is a derived unit.

9. The unit of Acceleration is a derived unit. Justify.

Answer:

Here,

Acceleration is defined as the rate of change of velocity with respect to time.

Formula of Acceleration,

Acceleration = Velocity/Time

Where, Velocity is measured in metres per second (m/s) and Time is measured in seconds (s).
So, the unit of acceleration becomes: m/s ÷ s = m/s² = ms⁻²

The unit m/s² or ms⁻² is not a base unit. It is formed combining two base units m and s. So, Acceleration is a derived unit.

10. The unit of Force is a derived unit. Justify.

Answer:

Here,

Force is a physical quantity that causes an object to accelerate or change its state of motion or shape.

According to Newton's Second Law of Motion: Force = Mass × Acceleration

Where Mass is measured in kilograms (kg) - base unit and Acceleration is measured in metre per second square (m/s²).

So,

The unit of force becomes:

Force = Mass × Acceleration = kg × m/s² = kg.m/s²

The derived unit is called the Newton (N).

Hence, 1 N = 1 kg.m/s²

Since the unit of force (newton) is expressed in terms of the base units kilogram, meter, and second, force is a derived unit in the SI system.

11. The unit of Density is a derived unit. Justify.

Answer:

Here,

The density of an object is the mass of the object compared to its volume.

We know,

Density = Mass/Volume

Where Mass is a base unit in the SI system, measured in kilograms (kg) and Volume is a derived quantity, measured in cubic meters (m³).

So, the unit of density becomes:

Density = Mass/Volume = kg/m³ = kg.m⁻³

This means the unit of density is kilogram per cubic meter (kg/m³) or (kg.m⁻³).

Since the unit of Density (

or d) is expressed in terms of the base units kilogram and meter Density is a derived unit in the SI system.

12. The unit of Pressure is a derived unit. Justify.

Answer:

Pressure is the force applied to the surface of an object per unit area over which that force is distributed.

We know,

Pressure = Force/Area

Where Force is a derived quantity which is measured in Newton (N) and Area is also derived quantity which is measured in square metre (m²).

So, The units of pressure becomes:

Pressure = N/m²

Since, 1 N = 1 kg⋅m/s²

Therefore,

1 Pa = 1 kg⋅m/s² ÷ m² = 1 kg/ms² = 1 kg.m⁻¹s⁻²

Hence, the unit of Pressure is Pascal (Pa), which is a derived unit.

The above Unit 1 Scientific Learning Class 10 Science and Technology Guide/note could be a valuable resource for both teachers and students.

Benefits for Teachers:

Structured Teaching: Provides a clear lesson structure, making teaching systematic and effective.
Key Points: Highlights important concepts to cover, ensuring comprehensive teaching.
Engaging Activities: Includes practical activities and experiments to make learning interactive.

Benefits for Students:

Easy Understanding: Simplifies complex concepts, making them easier to grasp.
Note-Making: Helps in creating organized and effective notes.
Exam Preparation: Offers practice questions and revision tips useful for terminal exams and SEE (Secondary Education Examination).

Importance of Using This Guide:

1. Clear Explanations: Breaks down difficult topics into understandable parts.
2. Consistent Learning: Ensures teachers and students are aligned on learning objectives.
3. Confidence Building: Regular practice and revision build exam confidence.
4. Real-Life Applications: Connects scientific concepts to daily life, enhancing interest and relevance.

Using this guide/note, both teachers and students can achieve a more effective and enjoyable learning experience, leading to better exam performance. Good Wishes!!

Tags

DR Gurung

A Learner (अज्ञान जस्तो ठूलो शत्रु अरु केही छैन।) 🙏🙏😍😍

Comments

First of all, thank you for taking the time to read my blog. It's much appreciated! If you would like to leave a comment, please do, I'd love to hear what you think!

Suggestions and/or questions are always welcome, either post them in the comment form or send me an email at drgurung82@gmail.com.

However, comments are always reviewed and it may take some time to appear. Always keep in mind "URL without nofollow tag" will consider as a spam. 😜

Newer Posts Older Posts